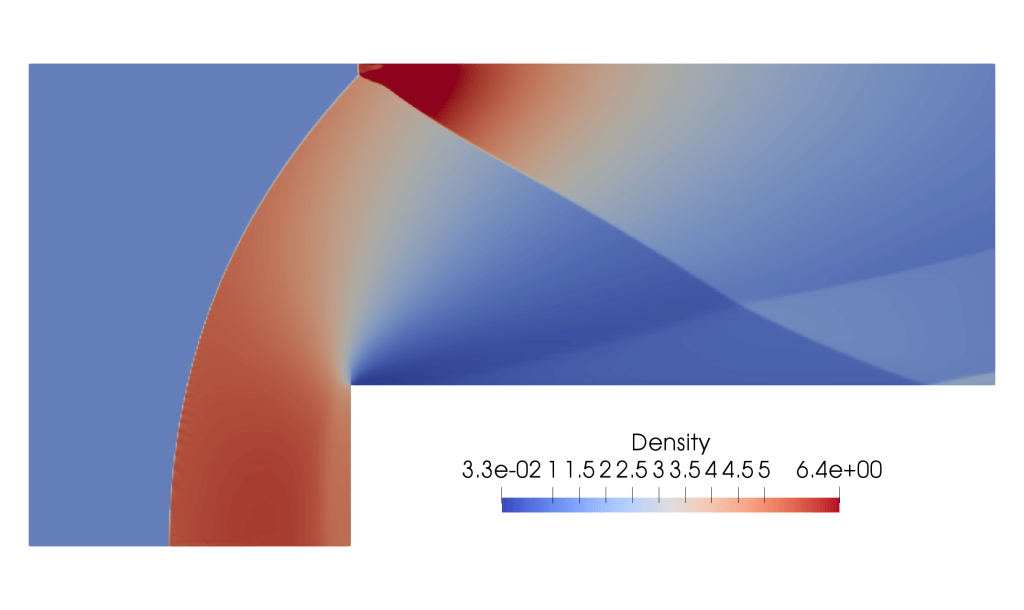This was a project in collaboration with J. Giesselmann. It was partially funded through the EPSRC grant EP/P000835/1.
Compressible fluid flows can be described by different models having different levels of complexity. One example consists of the compressible Euler equations which are the limit of the Navier-Stokes-Fourier equations when heat conduction and viscosity go to zero. Arguably the Navier-Stokes-Fourier system provides a more accurate description of reality since viscous effects which are neglected in Euler’s equation play a dominant role in certain flow regimes like thin regions near obstacles, for example, aerofoils exhibiting Prandtls’s boundary layers. However, viscous effects are negligible in large parts of the computational domain where convective effects dominate. Thus, it is desirable to avoid the effort of handling the viscous terms in these parts of the domain, that is, to use the Navier-Stokes-Fourier system only where needed and simpler models, e.g., (linearised) Euler equations, on the rest of the computational domain.
The approach we utilise here aims at having an a posteriori criterion which enables an automatic and adaptive choice of domains.
The following examines the use of model adaptivity on the Isothermal Navier-Stokes system in a situation where Karman vortices are produced by a flow over a cylinder.
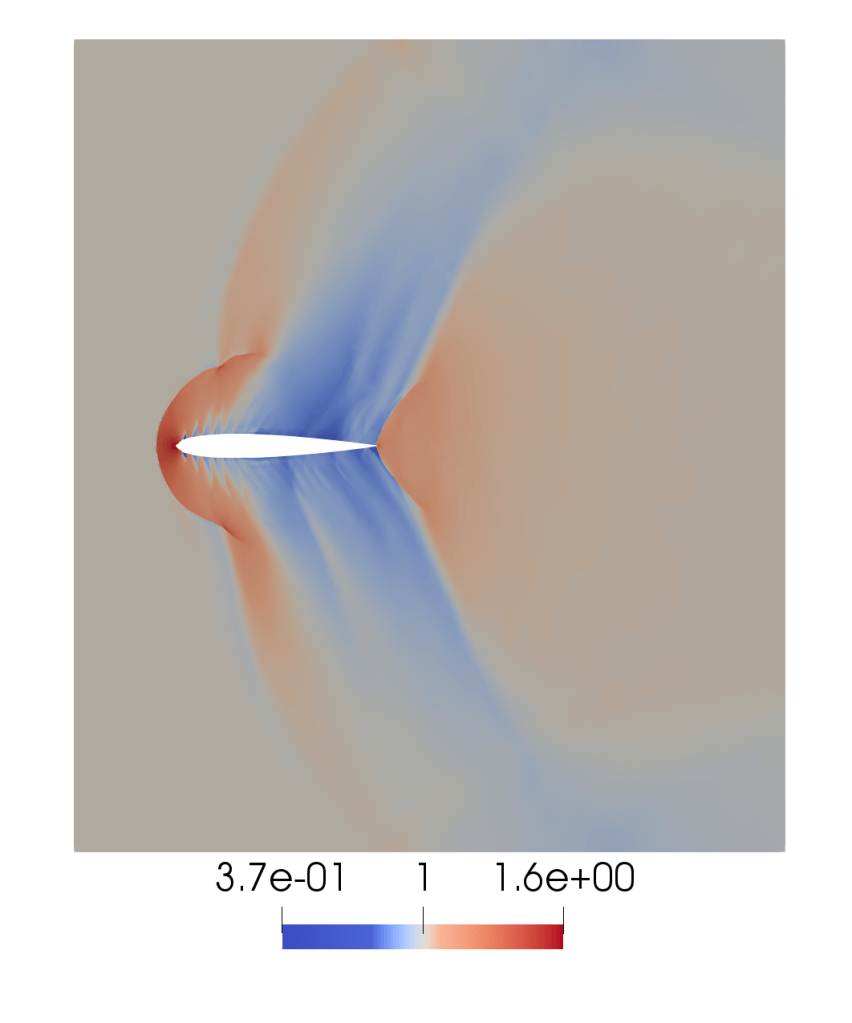
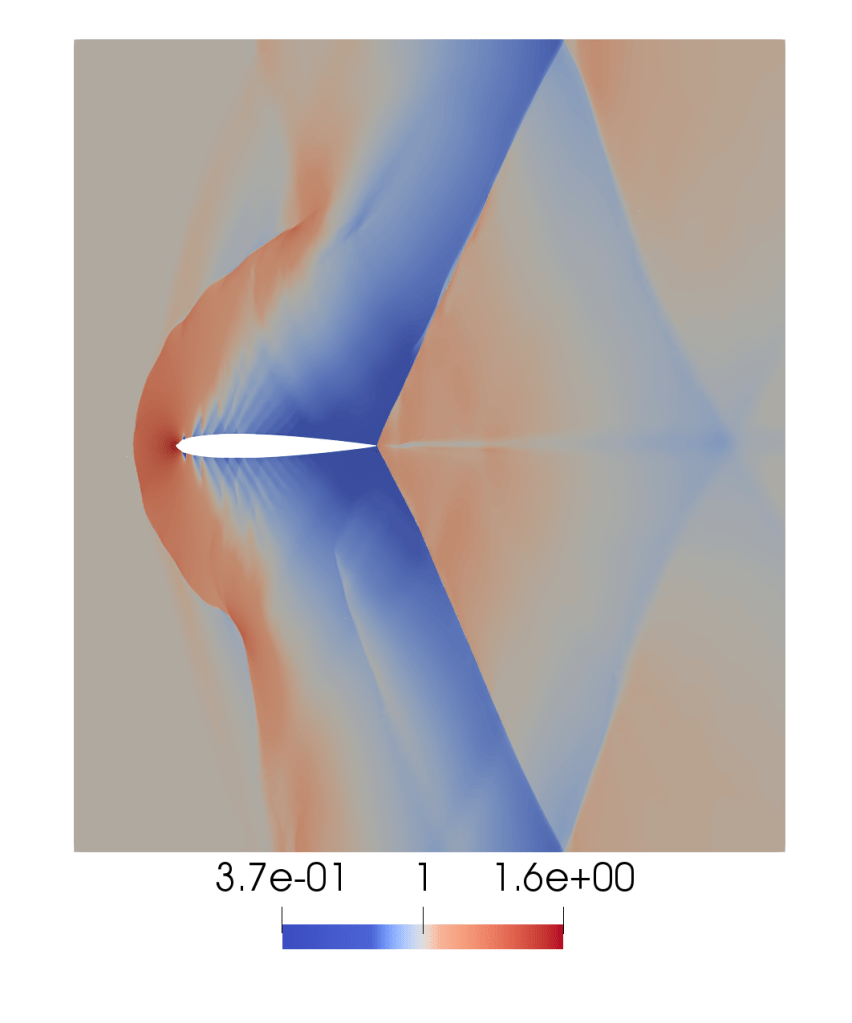
We used data from the Langely Research Centre website to construct a NACA 0012 aerofoil and simulated flow over this at Mach 1.02. Notice the bow shock before the aerofoil and trailing shocks in the wake.
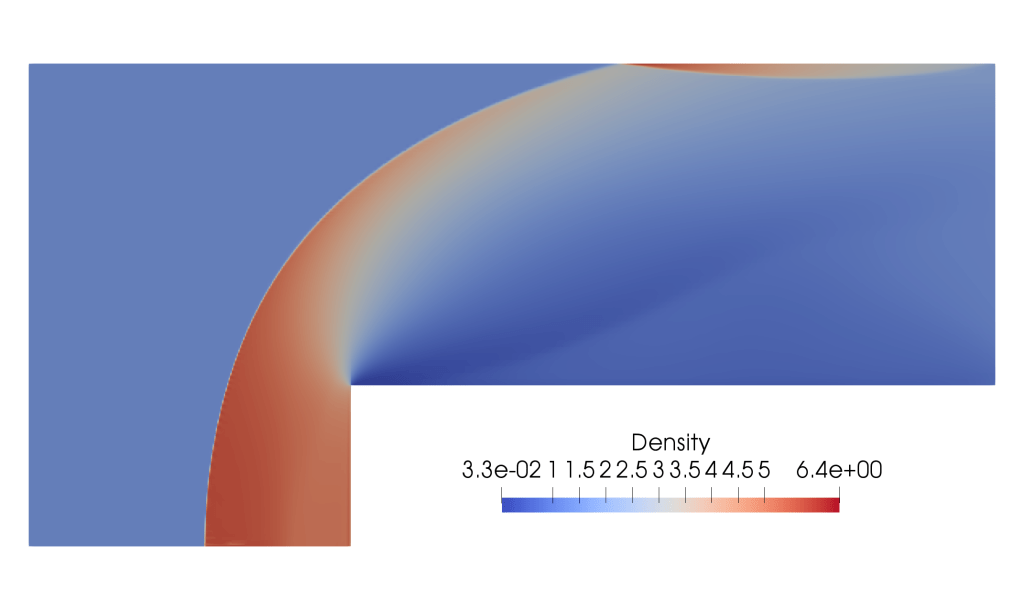
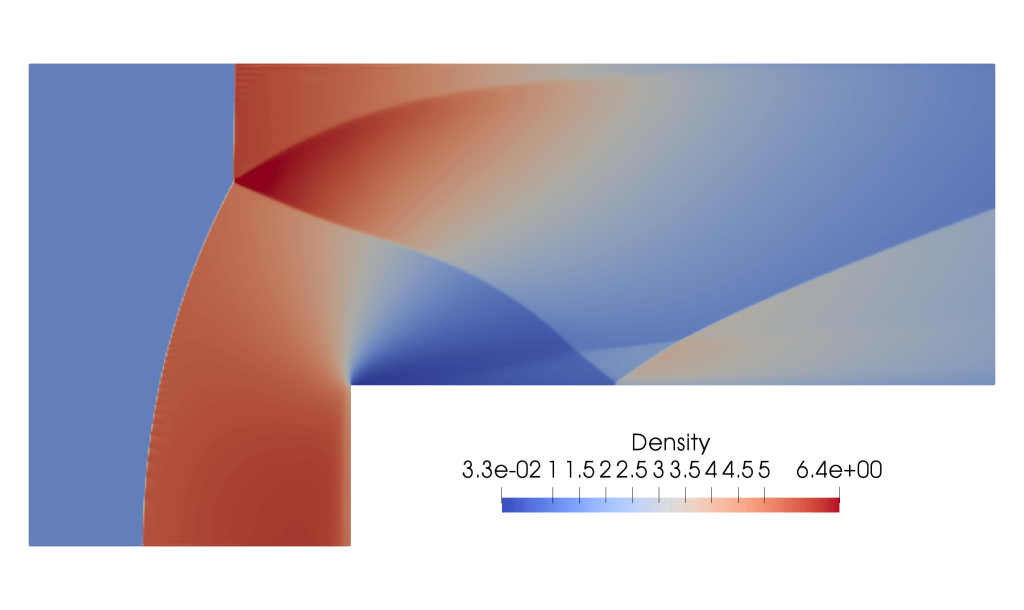
A forward facing step problem at Mach 3.66.